The integration by parts formula can also be written more compactly, with u substituted for f (x), v substituted for g (x), dv substituted for g' (x) and du substituted for f' (x) ∫ u dv = uv − ∫ v duIntegrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;In this tutorial you are shown how to do integrals of the above form

Ex 7 6 24 Integrate E X Sec X 1 Tan X Dx Is A E X Cos X
How to get f'(x)
How to get f'(x)-Integration of f' (x)/f (x) Some fractional expressions may appear too difficult to handle However with a bit of clever manipulation we may be able to put them in the form Now we know from differential calculus that Thus EXAMPLE 1 EXAMPLE 2This says that if f(x) is the rate of change of some known antiderivative F(x), then the integral of f(x) is the cumulative total change of F(x) F0(x) = f(x) =) Z b a f(x)dx = F(x)jx=b x=a = F(b) F(a) (The First Fundamental Theorem says that the de nite integral gives an antiderivative even if there is no formula F(x) de ning I(x) = R x




Unit 4 Integration B C A Study
Integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;Cf x dx c f x dx Standard Integration Techniques Note that at many schools all but the Substitution Rule tend to be taught in a Calculus II class For vertical axis of rotation ( 0xa and 0xa ) interchange x and y to get appropriate formulasIn Chapter 9, numerical integration formulas are used to derive the predictorcorrector methods for solving differential equations 41 Introduction to Quadrature We now approach the subject of numerical integration quadrature formulas are Z x 1 x0 f(x)dx
F(xh) F(x) h = f(x) 5The second fundamental theorem of integral calculus We are nowin a position toprove the final andmost important theorem in this sequence ofresults Theorem Let f(x) be a continuous function on the interval a,b Let G(x) be any function withthe property that G · (x) = f(x) Then ∫b a f(x)dx = G(b) G(a)Solution Observe that the derivative of x2 1 x 2 1 is 2x 2 x So, we will proceed with integration by substitution Let x2 1 = z x 2 1 = z Then, 2xdx = dz 2 x d x = d z ∫ f (x)dx = ∫ 2xsin(x21)dx = ∫ sinzdz = −cosz C = −cos(x2 1)C ∫ f ( x) d x = ∫ 2 x sin ( x 2 1) d x = ∫ sin Hence, the integrand is of the form e x f(x) f '(x) Therefore, using equation (2), we get ∫ e x (sin x cos x) dx = e x sin x C Question 2 Find ∫ e x (1 / x) – (1 / x 2) dx Answer Let, f(x) = 1/x Therefore, f '(x) = df(x)/dx = d(1/x)/dx = 1/x 2 Hence, the integrand is of the form e x
· Dec , 14 The integral is x ⋅ sin(x) cos(x) C You can get this result Integrating by Parts In general if you have the product of two functions f (x) ⋅ g(x) you can try this method in which you have ∫f (x) ⋅ g(x)dx = F (x) ⋅ g(x) − ∫F (x) ⋅ g'(x)dx The integral of the product of the two functions is equal to theThe derivative is then $$f'(x)= \sum_{\infty}^\infty 2 \pi n i c_n e^{2 \pi n i x},$$ so that $$f'(1x)=\sum_{\infty}^\infty2 \pi n i c_ne^{2 \pi n i x} $$ When multiplying $f(x) \cdot f'(1x)$ and integrating over the period, only the constant coefficient is of interest · A definite integral, in two dimensions, gives the area that exists under a curve between two endpoints For example, let us take the function f (x) = x 2 10 and the end points 2, 2 We could find the area under this curve using an indefinite integral Integration is a very powerful tool that allows us to solve a wide range of problems




Integration Formulas Trig Definite Integrals Class 12 Pdf



Numerical Differentiation Wikipedia
5/5/21 · List Of Integration Formulas Integral Formulas List We know that integration is the opposite of differentiation so we can write the basic integration formula as \(\frac{\mathrm{d} }{\mathrm{d} x}F(x)=f(x)\);Integrals cannot distinguish between this and f(x) Because all the functions in question are 2ˇperiodic, we can integrate over any convenient interval of length 2ˇ If f(x) is an odd function, so is f(x)cos(nx), and so a n = 0 for all n 0 If f(x) is an even function, then f(x)sin(nx) is odd, and so b n = 0 for all n 1 Daileda Fourier Coe cients(10) Z x a2 x2 dx= 1 2 lnja2 x2j (11) Z x2 a 2 x dx= x atan 1 x a (12) Z x3 a 2 x dx= 1 2 x2 1 2 a2 lnja2 x2j (13) Z 1 ax2 bx c dx= 2 p 4ac b2 tan 1 2ax b p 4ac b2 (14) Z 1 (x a)(x b) dx= 1 b a ln a x b x;




Misc 43 If F A B X F X Then X F X Dx Is Miscellaneous
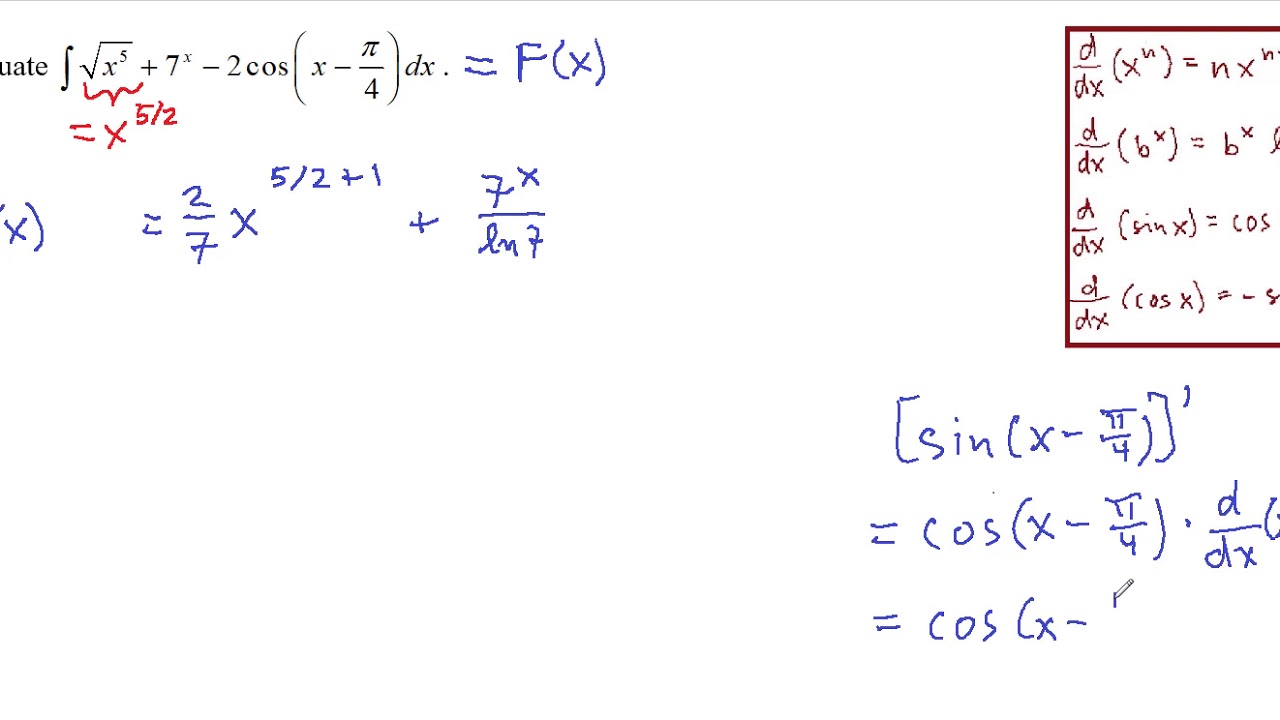



Indefinite Integrals
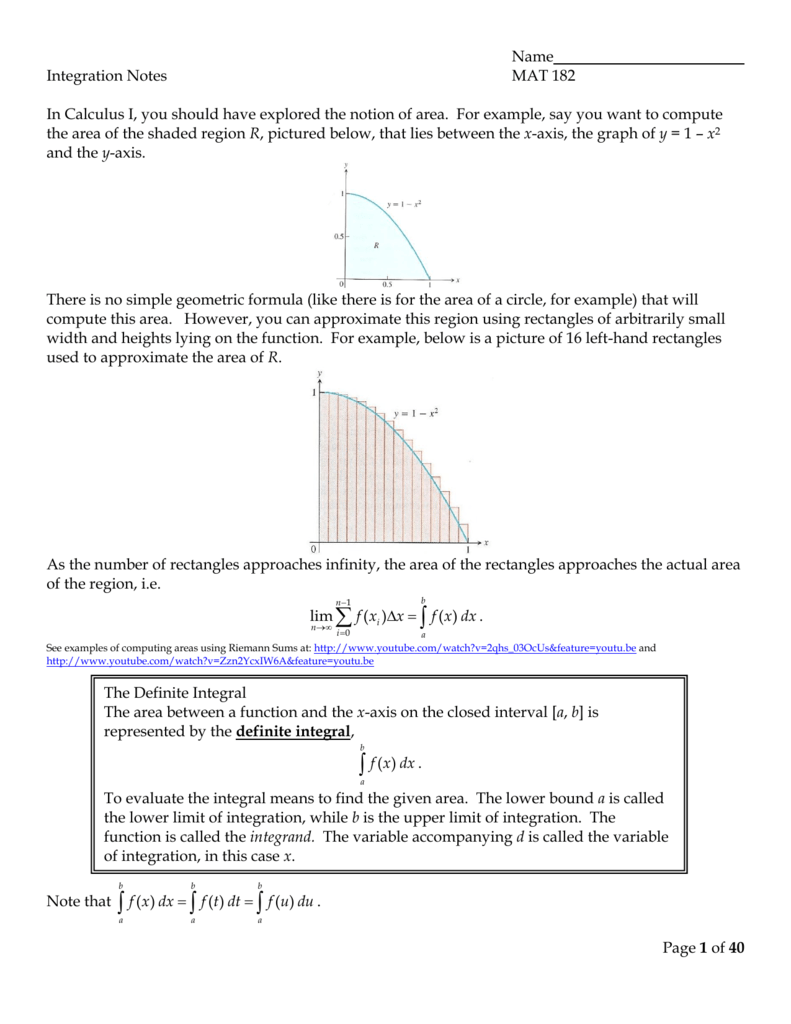
Dy f x dx we can find the antiderivative of both sides using the integration symbol ³ That is, y dy f x dx F x C ³³ Each piece of this equation has a name that I will refer to The integrand is f(x), the variable of integration is given by dx, the antiderivative of f(x) is F(x), and the constant of integration is C The termThe integrand is the product of two function x and sin (x) and we try to use integration by parts in rule 6 as follows Let f(x) = x , g'(x) = sin(x) and therefore g(x) = cos(x) Hence ∫ x sin (x) dx = ∫ f(x) g'(x) dx = ( f(x) g(x) ∫ f'(x) g(x) dx) Substitute f(x), f'(x), g(x) and g'(x) by x , 1, sin(x) and cos(x) respectively to write the integral as = x ( cos(x)) ∫ 1 ( cos(x)) dx Use formula 22 in in the table of integral formulas to evaluate ∫ cos(xIntegration of a function Method 1 Hence =∫ ≈ ∫ b a b a I f (x)dx f 2 (x) dx where f 2 (x) is a second order polynomial given by 2 f 2 = 0 1a 2 x One could even use the Lagrange polynomial to derive Simpson's formula Notice any method of threepoint quadratic interpolation can be used to accomplish this task




Answered Verify The Formula F Nds Div F Dv G Bartleby




Integration Formulas Trig Definite Integrals Class 12 Pdf
Students the standard derivation of the Integration by Parts formula as presented in 1 By the Product Rule, if f (x) and g(x) are differentiable functions, then d dx f (x)g(x) = f (x)g (x) g(x)f (x) Integrating on both sides of this equation, f (x)g (x) g(x)f (x) dx = f (x)g(x), which may be rearranged to obtain f (x)g (x)dx = f (x)g(x)− g(x)f (x)dxThe product rule of integration for two functions say f(x) and g(x) is given by f(x) g(x) = ∫g(x) f'(x) dx ∫f(x) g'(x) dx22/8/19 · Chapter 7 Class 12 Integration Formula Sheet by teachoocom Basic Formulae = ^( 1)/( 1) , 1 , = = sin x C = cos x C 2 = tan x c 2 = cot x c = sec x c
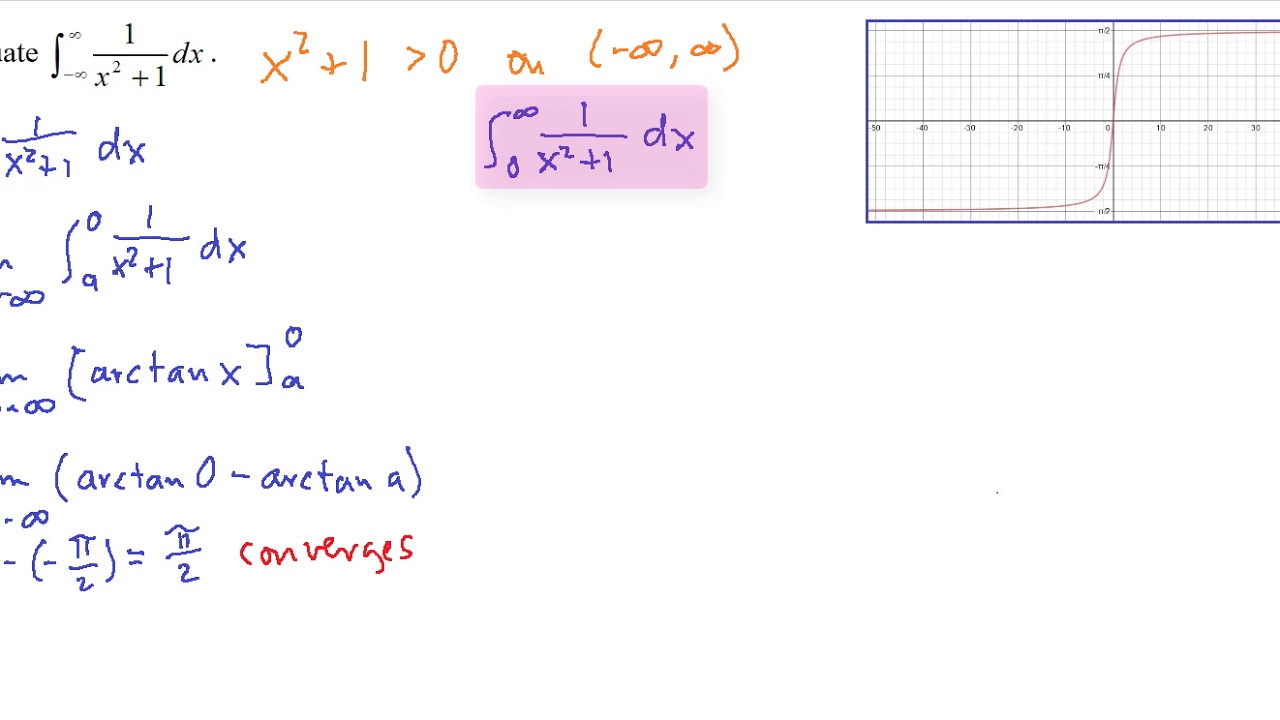



Improper Integrals




Integration Of The Form F X F X Dx
For convenience, if F x( ) f x( ) dx d = , then we write ∫ f x( ) dx = F x( ) C → The constant C is called the constant of integration , and it is arbitrary in nature → The sign ∫ is called the integral sign , and f x ( ) is called the integrand Quick Example As x x dx d 4 1 2 = , we have C x dx x ∫ = 4 2 1 F(x)C f (x) differentiation2 f x e x3 ln , 1,0 Example Use implicit differentiation to find dy/dx given e x yxy 2210 Example Find the second derivative of g x x e xln x Integration Rules for Exponential Functions – Let u be a differentiable function of x 1Then we can write \(\int f(x)\dx=F(x)C\) Students can check all the formulas of integration chapters




Functions Defined By Integrals Switched Interval Video Khan Academy




Consider Integrals I F Integral 0 1 F X Log Chegg Com
17/4/18 · If ???f(x)=f(x)???, the function is odd If we discover that the function is even or odd, the next step is to check the limits of integration (the interval over which we're integrating) In order to use the special even or odd function rules for definite integrals, our interval must be in the form ???a,a???So in order to integrate a function of the form $e^{f(x)}$, let $u=f(x)$, and thus $du=f'(x)dx$, which allows you to 'solve' for $dx$ in terms of $du$ Then your original integral goes from $$ \int e^{f(x)}dx $$ to $$ \int \frac{e^u}{f'(x)}du $$ Of course, this is not always so easy to integrate, as Moron points outExample showing the use of the modulus sign




Ex 7 6 24 Integrate E X Sec X 1 Tan X Dx Is A E X Cos X




Formula Sheet For Integration Notes
The simple trapezium formula calculates the integral of a function f (x) as the area under the curve representing f (x) by approximating it with the sum of trapeziums The area of each trapezium is calculated as width times the average height ExampleThe formula for integration by parts is the following ∫ f(x)g′(x) = f(x)g(x)−∫ f′(x)g(x) ∫ f (x) g ′ (x) = f (x) g (x) − ∫ f ′ (x) g (x)29/1/13 · what we're going to do in this video is review the product rule that you probably learned a while ago and from that we're going to derive the formula for integration by parts which could really be viewed as the inverse product rule integration by parts so let's say that I start with some function that can be expressed as the product f of X it can be expressed as a product of two




Misc 43 If F A B X F X Then X F X Dx Is Miscellaneous




How To Do Integrals Of The Form F X F X Examsolutions Maths Problems Answered Youtube
Standard Integration Techniques ∫ f x dx represents the net area between f x( ) and the xaxis with area above xaxis positive and area below xaxis negative Area Between Curves The general formulas for the two main cases for each are, The two main formulas are V A x dx=PART I Numerical Integration NewtonCotes Integration Formulas The idea of NewtonCotes formulas is to replace a complicated function or tabulated data with an approximating function that is easy to integrate I = Z b a f(x)dxThe definite integral f(k) is a number that denotes area under the curve f(k) from k = a and k = b A definite integral retains both lower limit and the upper limit on the integrals and it is known as a definite integral because, at the completion of the problem,




Integration Formulas Trig Definite Integrals Class 12 Pdf




Riemann Integral Wikipedia
· Now this will get converted into entities One of the integration can be obtained from above formula and one from $\int f(x)^n f^{'} x dx = \frac { f(x)^{n1}}{n 1 } , n \ne 1 $ Integration of Rational algebraic functions using Partial FractionsMath\int e^x(f(x)f'(x))dx = \int e^xf(x) e^xf'(x)dx/math Let mathg(x) = e^x/math mathg'(x) = e^x/math math\int e^x(f(x)f'(x))dx = \int g'(x)f(x)f28/5/17 · One way to find the integral of x e x is to use the product rule and then integrate This is how the integration by parts formula is derived In this lesson, we
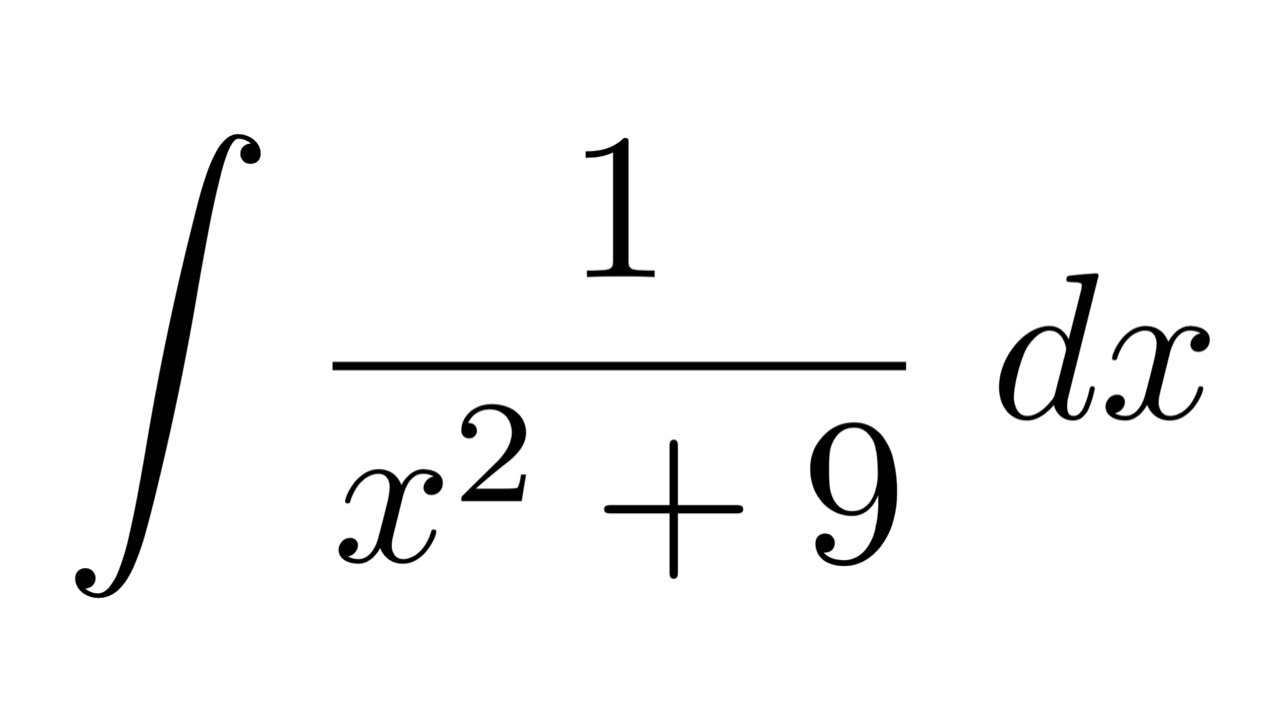



Integral Of 1 X 2 9 Substitution Youtube




Solved 1 Point Integration By Parts Indefinite Integr Chegg Com
Integration Formulas 1 Common Integrals Indefinite Integral Method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = Integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − Integrals of Rational and Irrational Functions 1 1 n x dx Cn x n = ∫ 1 dx x Cln x ∫ = ∫cdx cx C= 2 2 x ∫xdx C= 3 2 3 x ∫x dx C= 2 1 1A6=b (15) Z x (x a)2 dx= a a xIn mathematics, a function is a binary relation between two sets that associates each element of the first set to exactly one element of the second set Typical examples are functions from integers to integers, or from the real numbers to real numbers Functions were originally the idealization of how a varying quantity depends on another quantity




Solved Consider The Following Function F X Integral X Chegg Com




Integrate By Parts
In this tutorial you are shown how to do integrals of the form f '(x) / f (x) Why the Modulus Sign?34) \\int {\csc {\text{h}}x\coth xdx = – \csc {\text{h}}x c} \ 35) \\int {\frac{1}{{\sqrt {{a^2} – {x^2}} }}dx = {{\sin }^{ – 1}}\frac{x}{a}} c\ orF(x)dx We assume that the values of the function f(x) are given at n 1 points x 0,,x n ∈ a,b Note that we do not require the first point x 0 to be equal to a, and the same holds for the right side of the interval Given the values f(x 0),f(x n), we can write the interpolating polynomial of degree 6 n, which in the Largenge form




Power Series And Polynomial Approximation




Integrate Synonym Integration Rules Integration Definition Another Word For Integrate Integrated Meaning The Int Studying Math Math Formulas Maths Formula
2/1/21 · Figure 711 To find the area of the shaded region, we have to use integration by parts For this integral, let's choose u = tan − 1x and dv = dx, thereby making du = 1 x2 1 dx and v = x After applying the integrationbyparts formula (Equation 712) we obtain Area = xtan − 1x1 0 − ∫1 0 x x2 1 dxIntegrate 1/(cos(x)2) from 0 to 2pi;I f (x)dx (1) Most (if not all) of the developed formulas for integration based on a simple concept of are approximating a given function f (x)by a simpler function (usually a polynomial function) f i (x) , where i represents the order of the polynomial function In apterCh 0703, Simpsons




Power Series And Polynomial Approximation




Pdf On The Fundamental Theorem Of P Q Calculus And Some P Q Taylor Formulas
Integral of exponential function a^x(with verification)「Kevin MacLeod」創作的「Meditation Impromptu 02」獲得「Creative Commons Attribution」的授權使用 (https//creativecoView more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn28/5/ · Integration Formulas Indefinite Integration If f and g are functions of x such that g'(x) = f(x) then, ∫ f(x)dx = g(x)c ⇔ d d x {g (x) c} = f (x) \frac{d}{dx}\left \{g(x)c \right \} = f(x) d x d {g (x) c} = f (x), where c is called the constant of integration Standard formula (a) ∫x n dx = x n 1 n 1 c \frac{x^{n1}}{n1




The Definite Integral And Ftc




All Integration Formulas Complete List Of Integrals Cuemath
This uses the product rule in reverse so to integrate f (x) * g' (x) you get f (x)g (x) integral (g (x)*f' (x)) If you can find the second integral you are done Otherwise the problem is more difficult




Integration Of E X Sin X Dx Teachoo Maths Integration Class 12




The Definite Integral And Ftc
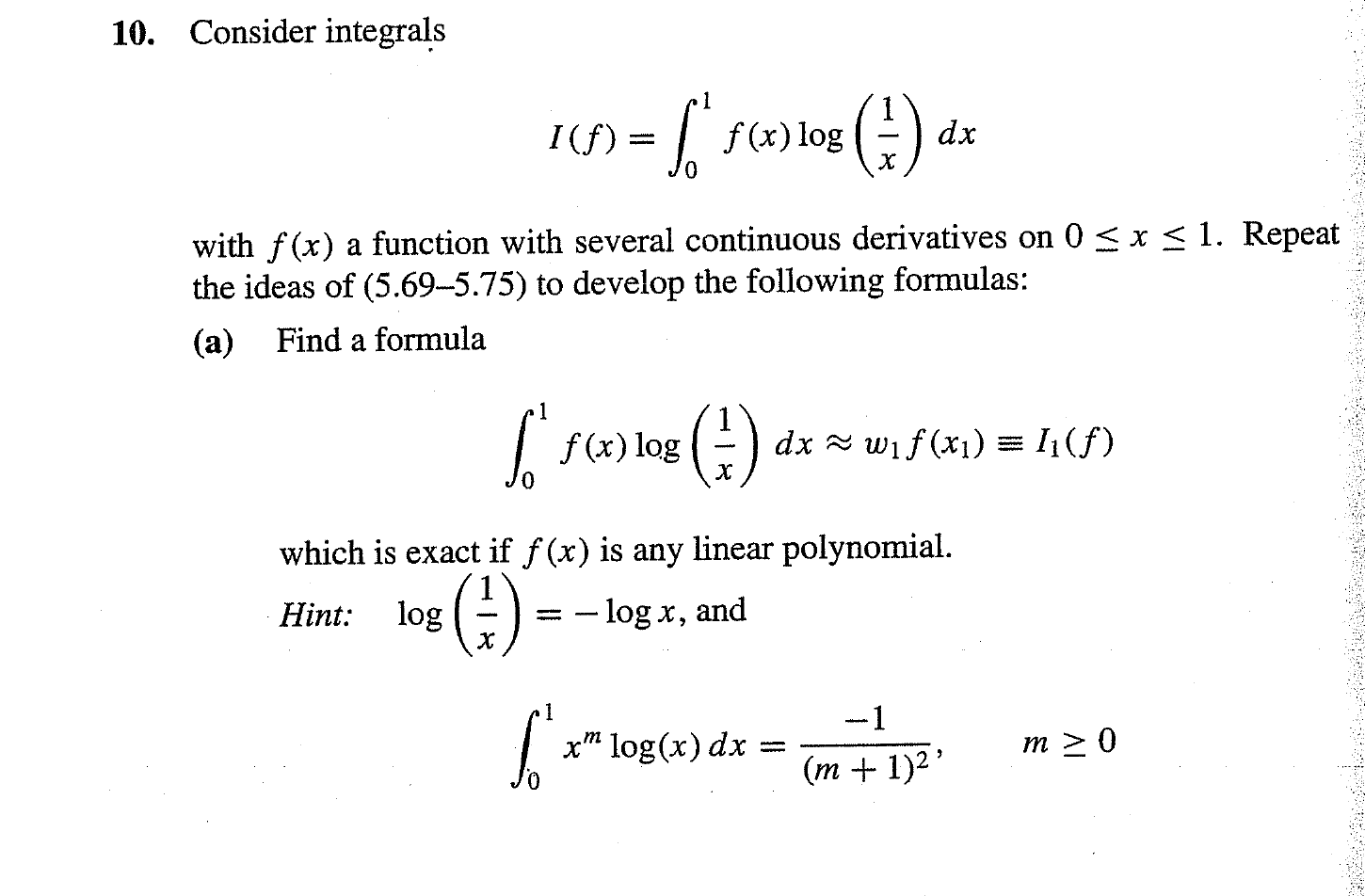



Consider Integrals I F Integral 0 1 F X Log Chegg Com




The Integral F X Dx Is To Be Approximated By The Chegg Com




Integration By Parts Introduction Youtube




The Definite Integral And Ftc
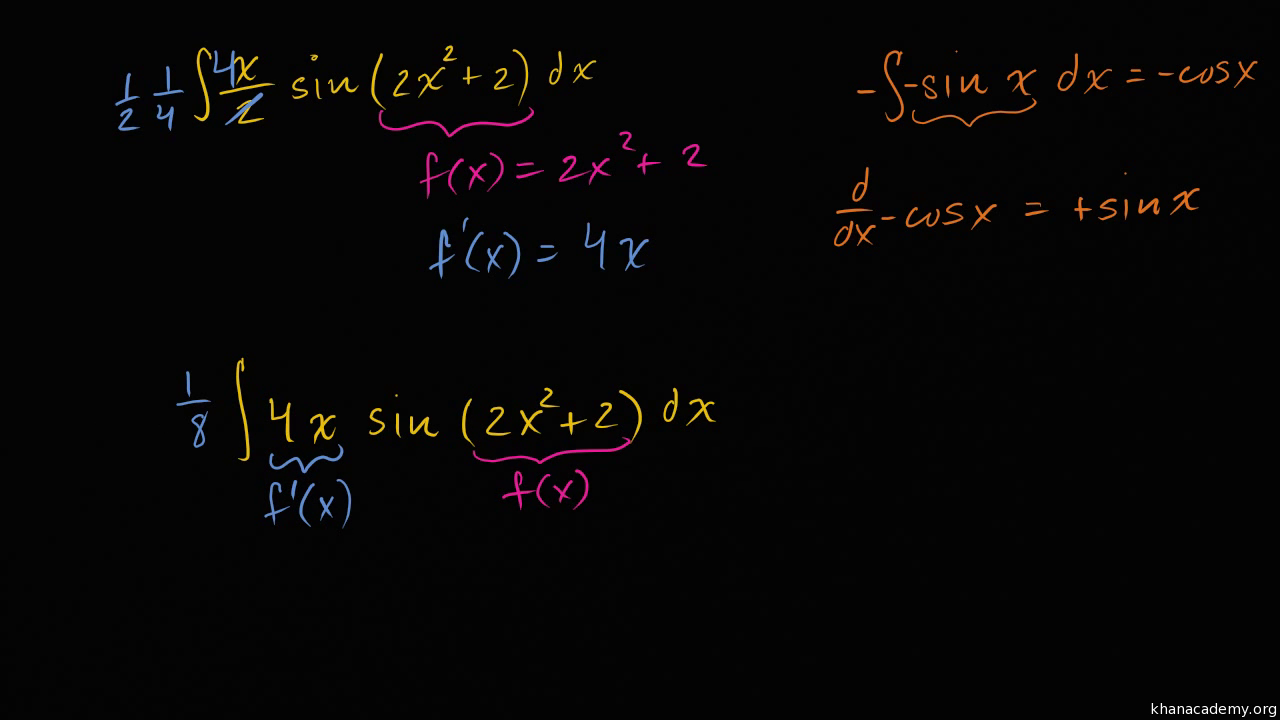



Reverse Chain Rule Example Video Khan Academy




Image2 Slideserve Com Integration By Pa




Solved Use All Three Point Formulas To Compute The Approx Chegg Com




Definite Integral 0 To 2a F X 2 0 To 2a F X If F 2a X F X And 0 If F 2a X F X Property Youtube
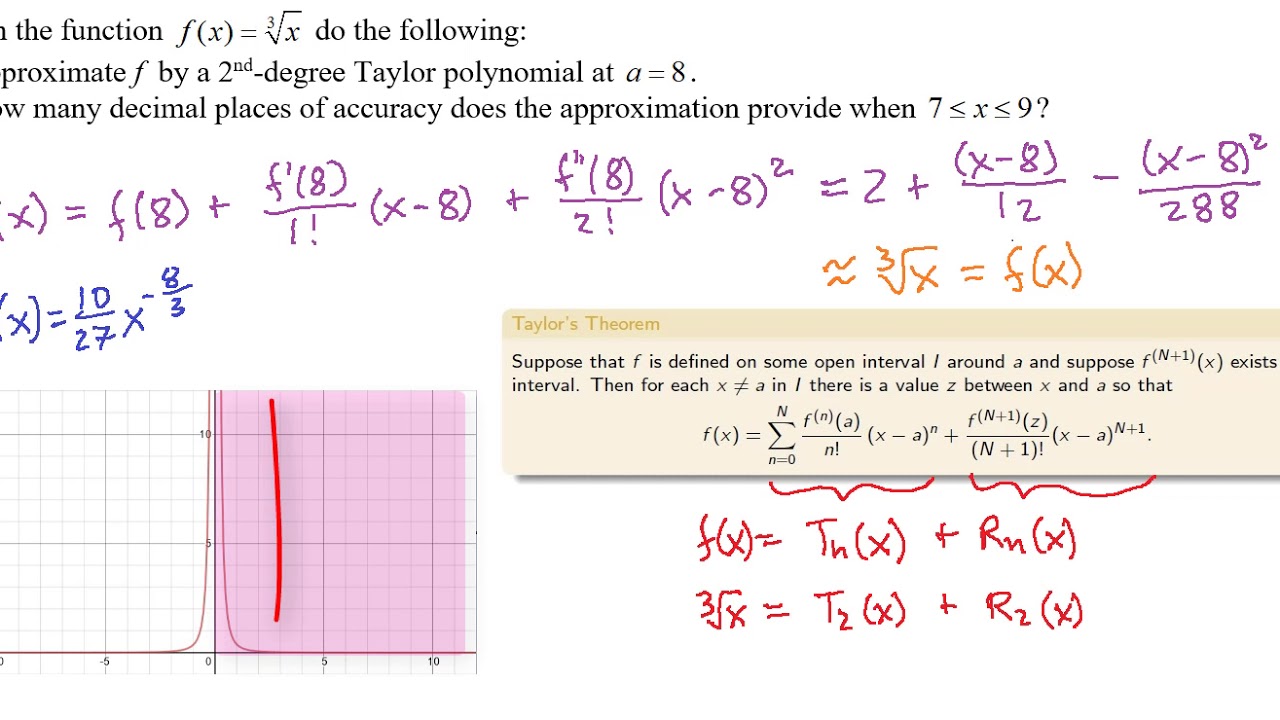



Power Series And Polynomial Approximation




Derivatives Of Inverse Functions Video Khan Academy




Derivative Of F X 1 X Using The Limit Definition Youtube




Solved G B F G T G T Dt F X Dr G A F G B Chegg Com




The Definite Integral And Ftc
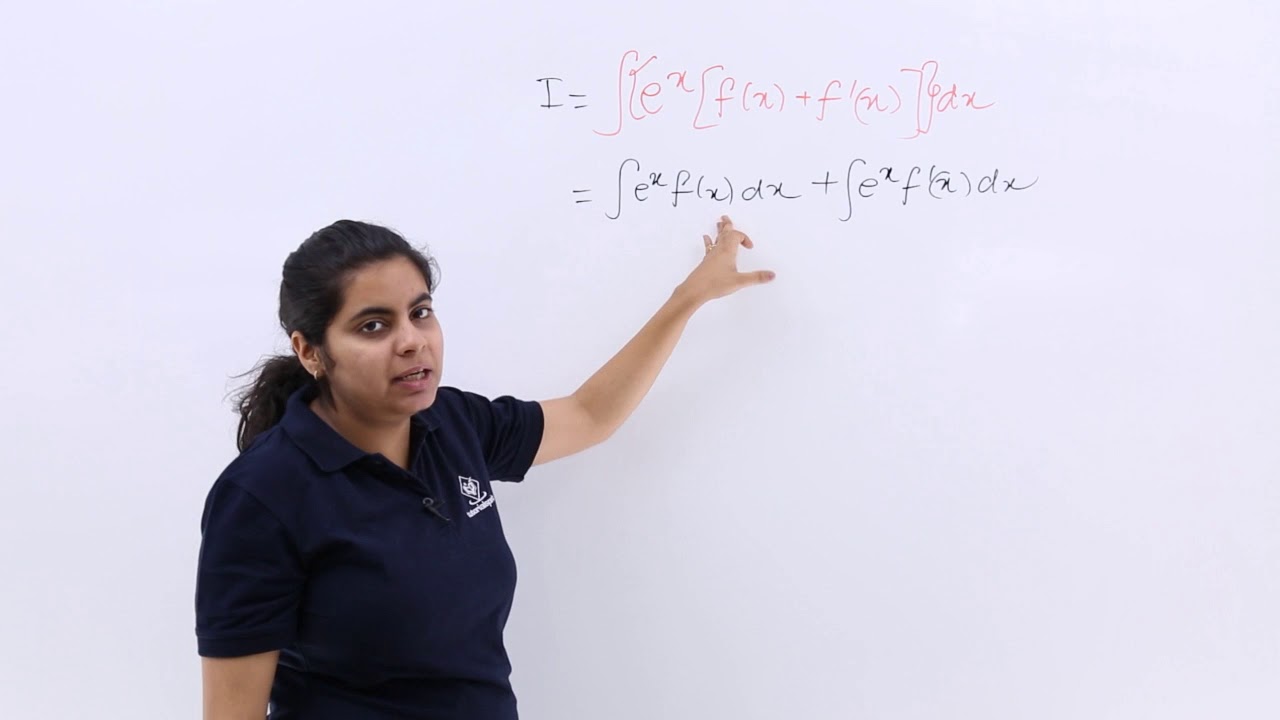



Integral Of E X F X F X Dx Youtube




Finding Derivative With Fundamental Theorem Of Calculus Video Khan Academy




The Gamma Function Gamma X Is An Integral Defined Chegg Com




Midpoint Derivative Based Closed Newton Cotes Quadrature Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub



Calculus Index Cards
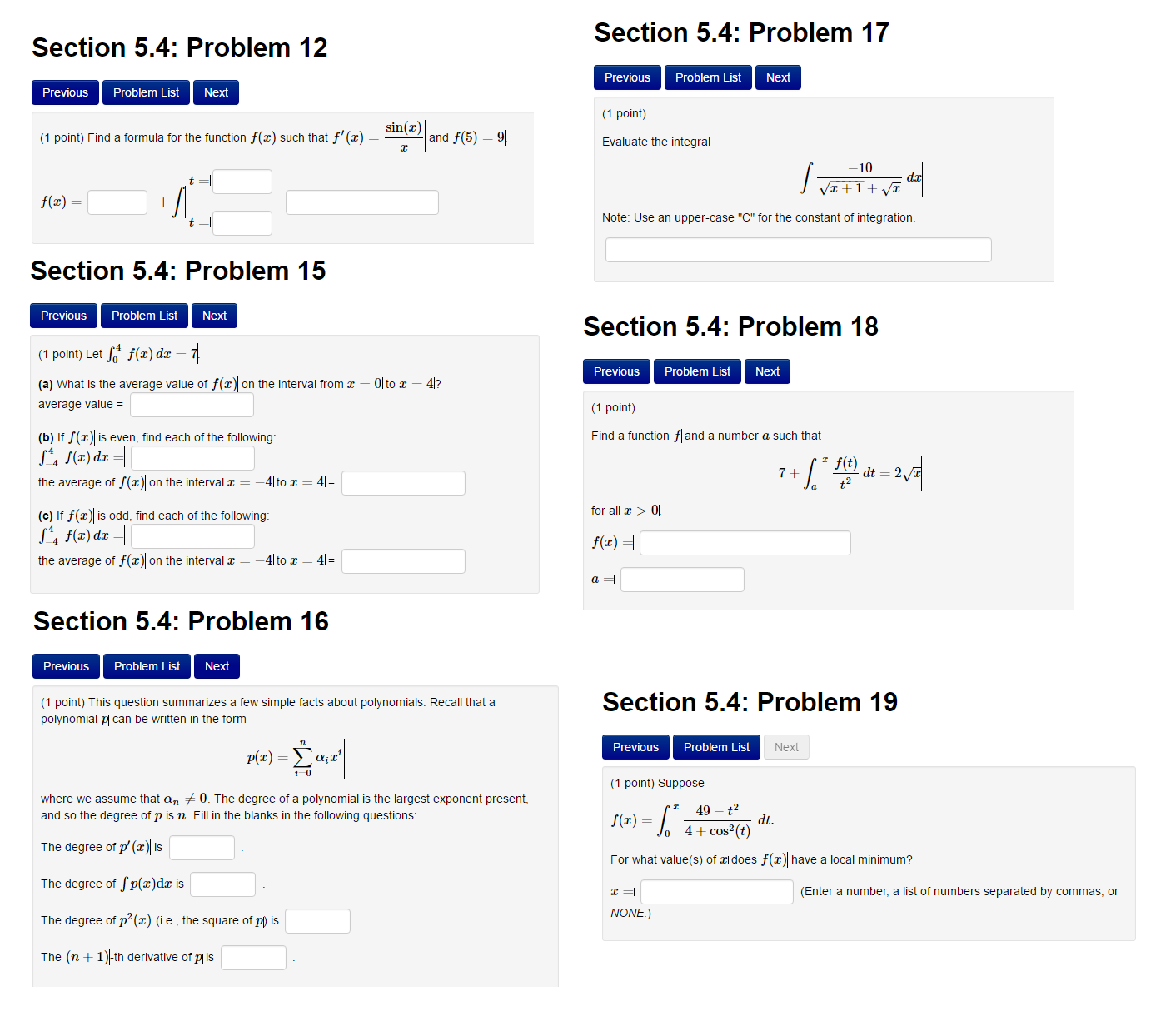



Find A Formula For The Function F X Such That F X Chegg Com




Evaluate Each Of The Following Integral Int A B F X F X F A B




7 Techniques Of Integration Copyright C Cengage Learning All Rights Reserved Slideshow And Powerpoint Viewer 7 1 Integration By Parts Copyright C Cengage Learning All Rights Reserved




Suppose We Define The Definite Integral Using The Following Formul




Integral Wikipedia




Ex 7 8 2 Integrate X 1 Dx From 0 To 5 By Limit As A Sum




Unit 4 Integration B C A Study




Ex 7 8 2 Integrate X 1 Dx From 0 To 5 By Limit As A Sum




Integrals Of The Form F X F X Examsolutions




Give The Formula To Exactly Evaluate Integral B A Chegg Com




Packet 21 Integration By Parts Ppt Download




Practical Integration By Parts Calculus
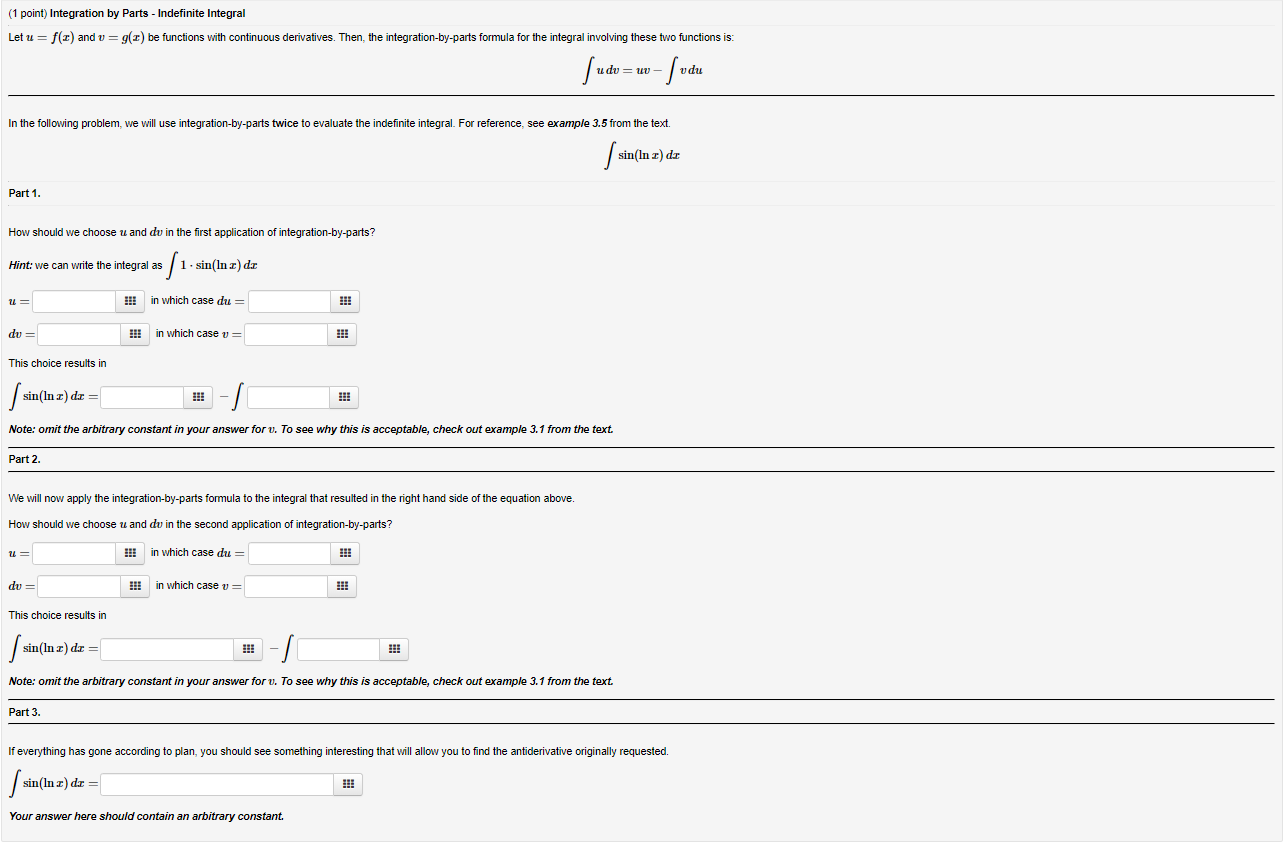



1 Point Integration By Parts Indefinite Integral Chegg Com




Ch 6 The Definite Integral Ppt Download




Integration By Parts Definite Integrals Video Khan Academy



Solved Given The Function F X 2x 1 Calculate The Area Between The Graph Of F And The X Axis On The Interval 1 3 Using Two Different Metho Course Hero




Example 26 Evaluate Integral Ex Dx As The Limit Of A Sum
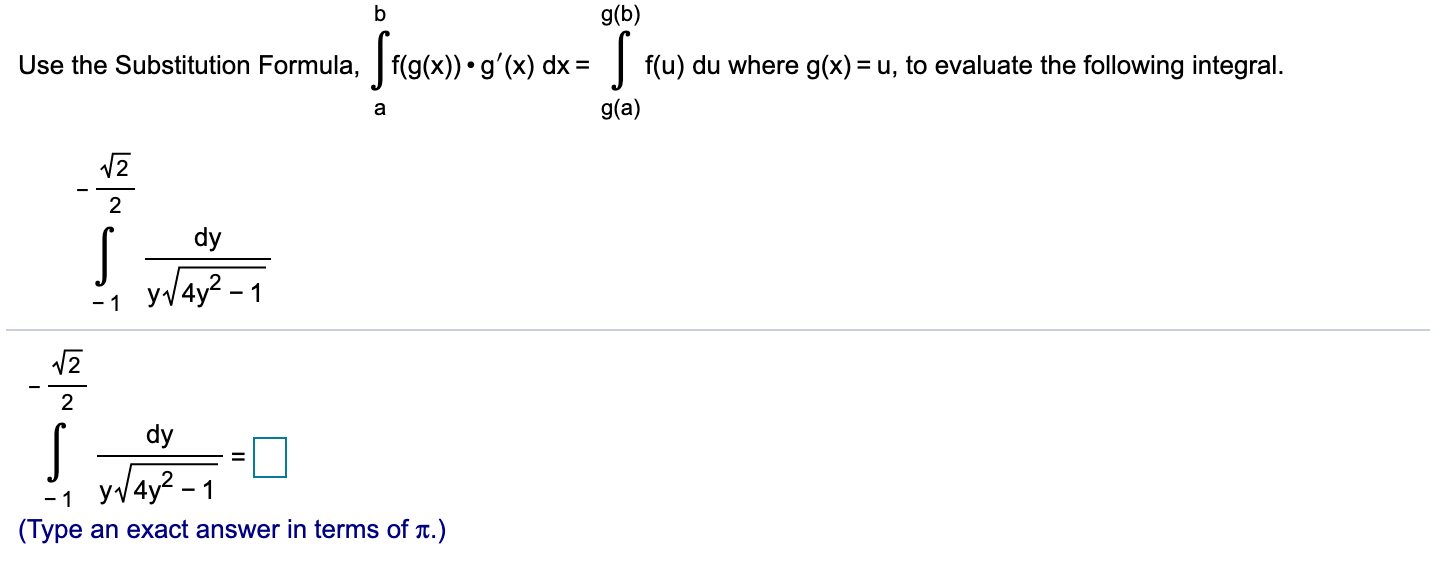



Answered B G B F G X G X Dx Use The Bartleby




Find Integration Lnx Or Log X Integration By Parts Teachoo



Document




Integration By Parts Intro Video Khan Academy
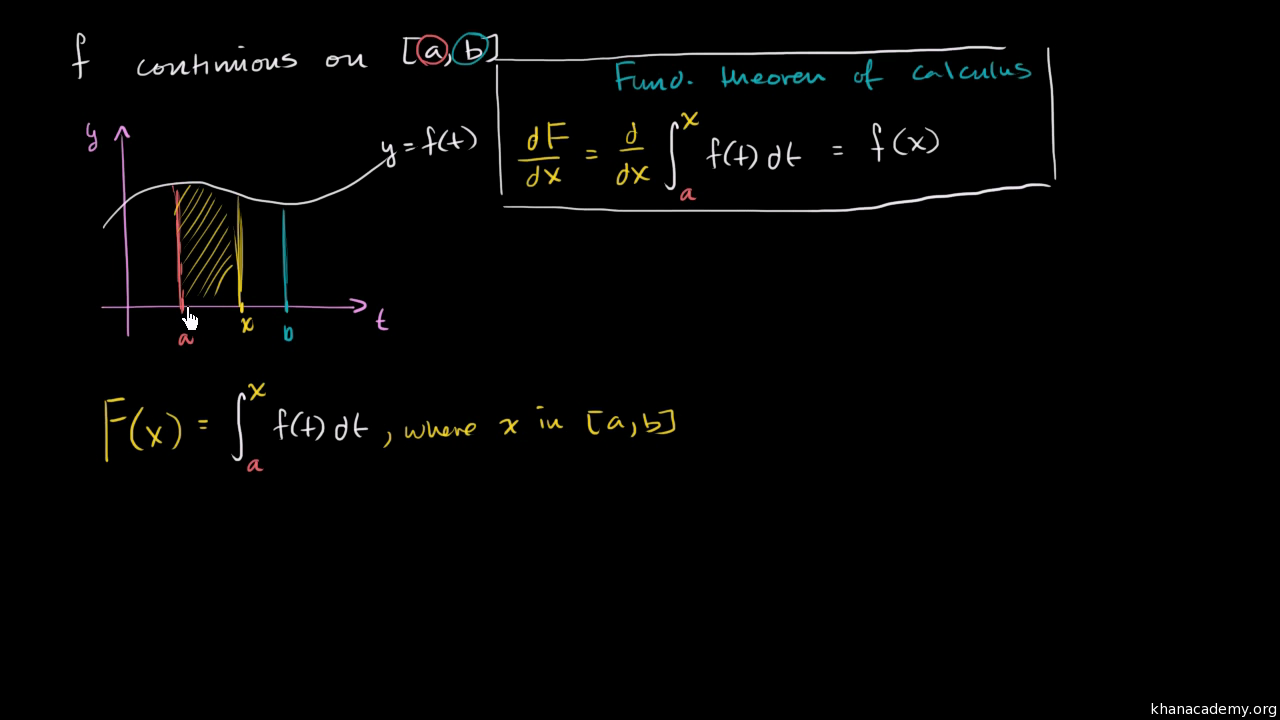



The Fundamental Theorem Of Calculus And Accumulation Functions Video Khan Academy




Pdf First Approximation Formula For A Definite Integral




All Integration Formulas Complete List Of Integrals Cuemath




Power Series And Polynomial Approximation




Answered B 14 N B A Use The Equation F X Dx Bartleby
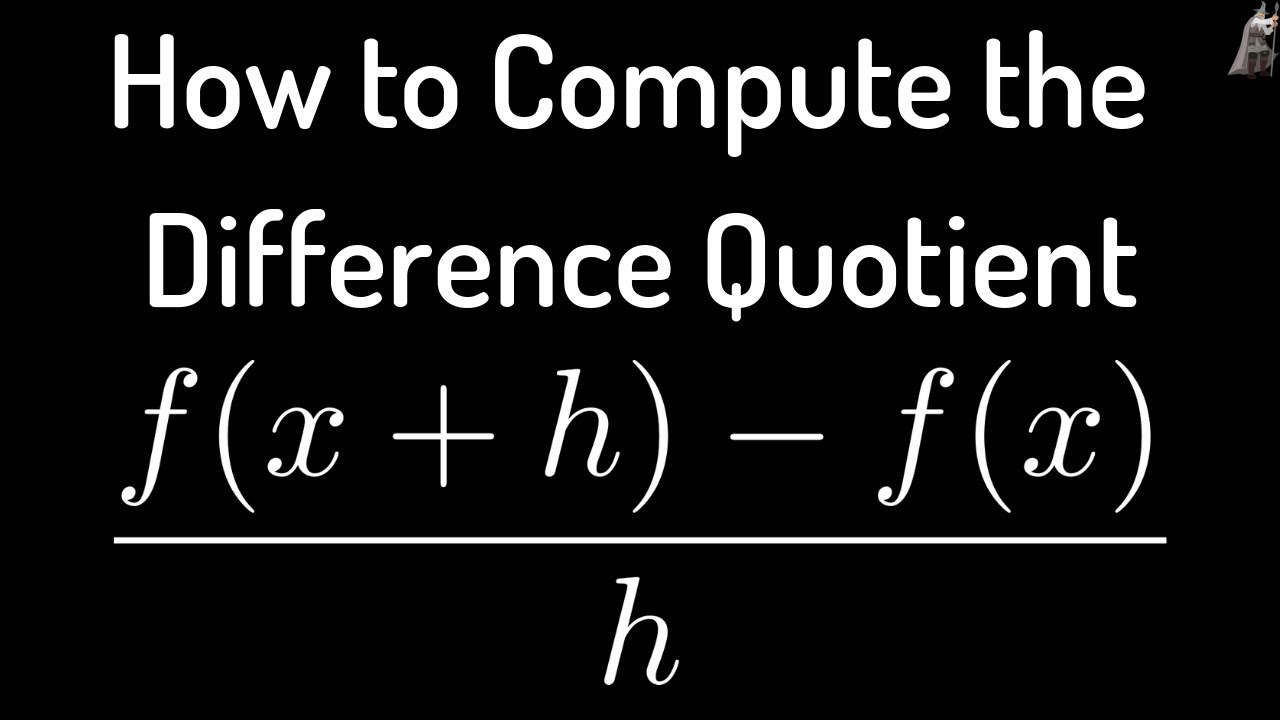



How To Compute The Difference Quotient F X H F X H Youtube




Ex 7 11 19 Show F X G X Dx 2 F X F X F A X Ex 7 11



Solved Consider The Function F X Graphed Below No Formula For This Function Is Provided Each A1 A3 And Is The Area Of The Shaded Regi Course Hero




Solved 1 Point Integration By Parts Indefinite Integr Chegg Com




The Third Calculus Competition Of Uw La Crosse



No comments:
Post a Comment